In 1994, Troy Brown was convicted of raping a 9-year-old girl in Carlin, Nevada. The conviction heavily relied on DNA evidence presented by the prosecution. The state’s expert, Renee Romero, testified that the DNA found at the crime scene matched Brown’s profile and claimed that the probability of a random person matching this profile was 1 in 3 million. This was misinterpreted as meaning there was only a 1 in 3 million chance that Brown was innocent—a classic example of the prosecutor’s fallacy. Based on this flawed statistical reasoning, the jury concluded Brown’s guilt. There was no other conclusive evidence linking Brown to the crime, and the conviction was based almost entirely on the misunderstood DNA statistics.
Explanation of Prosecutor’s Fallacy
Imagine this scenario:
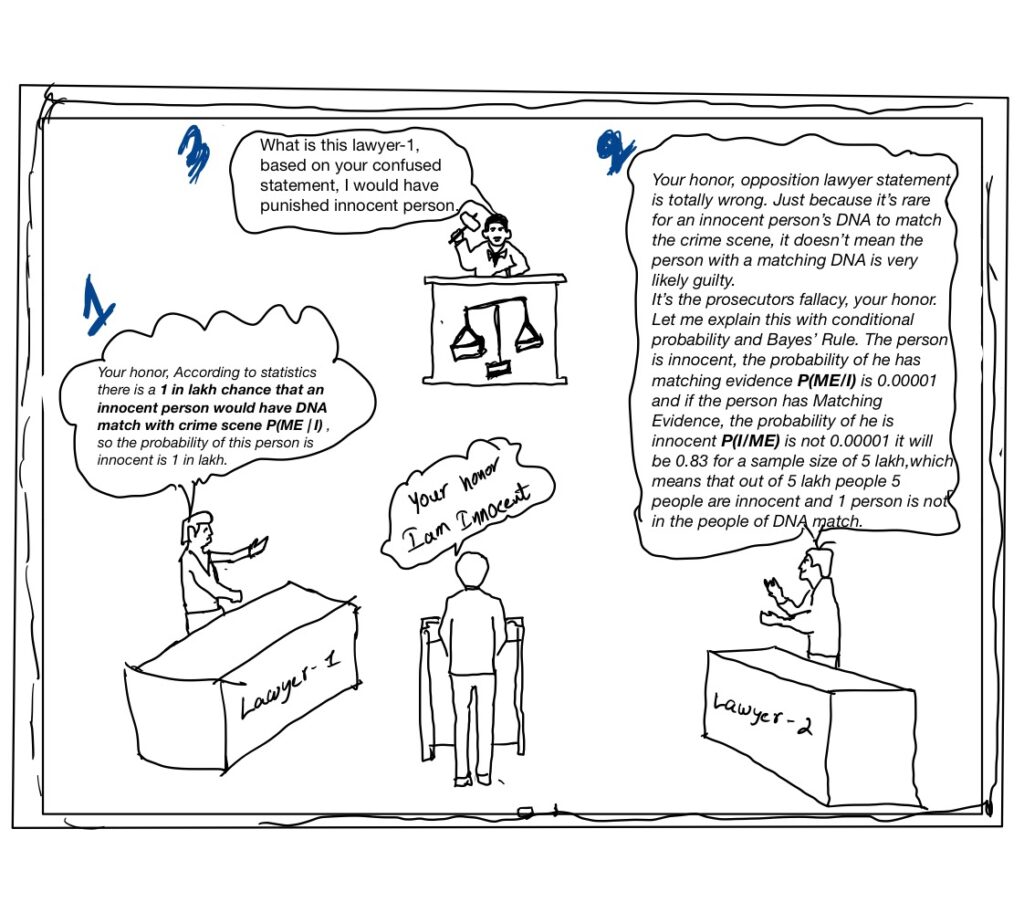
A murder has occurred in your locality, which has a population of 5 lakh. Only one person is guilty. Unfortunately, you are innocent but your DNA matches the DNA found at the crime scene. The verdict is based solely on this DNA evidence. According to statistics, there is a 1 in lakh chance that a random (innocent) person’s DNA would match the crime scene DNA. Unfortunately, you are that one unlucky person. While presenting the case, the opposing prosecutor says: “Your honor there is a 1 in lakh chance that a random person (an innocent person) would have a DNA match with the crime scene. So, the probability that he is innocent is 0.00001.”
There is no other evidence to prove your innocence.
Let’s now break down the prosecutor’s statements.
The actual statistical statement is:
There is a 1 in 100,000 chance that an innocent person’s DNA matches the crime scene DNA.
Here, I am referring to the crime scene DNA match as the event “Matching Evidence” (ME).
In the above statement we already know that you are innocent, and the probability of you having matching evidence (i.e., a DNA match) P(ME | I) is 1/100,000.
But the prosecutor’s statement is:
The person has matching evidence(we already know), so the probability that he is innocent P(I | ME) is 1/100,000.
In this statement we only know you have Matched Evidence (DNA match with crime scene DNA), the probability of you are innocent P(I | ME) was not known.
Lets Understand the difference between P(I | ME) and P(ME | I)
What are P(I | ME) and P(ME | I)?
P(I | ME) and P(ME | I) are conditional probabilities.
Let’s say there are two events: A and B.
- P(A | B) means event B has already occurred, and we are calculating the probability of event A occurring after event B occurring.
- $$ P(A | B) =\frac{ P(A \cap B)}{ P(B)} $$
- P(B | A) means event A has already occurred, and we are calculating the probability of event B occurring after event A occurring.
- $$ P(B | A) =\frac{ P(A \cap B)}{ P(A)} $$
- Equating $P(A \cap B)$ from P(A | B) and P(B | A), we get the Bayes’ Rule
- $$ P(A | B) = \frac{P(B | A) P(A)}{P(B)}$$
In same way
- P(I | ME) means: Given that there is a DNA match with the crime scene, what is the probability that the person is innocent?
- P(ME | I) means: Given that the person is innocent, what is the probability that their DNA matches the crime scene
The prosecutor totally misunderstood conditional probabilities P(I | ME) and P(ME | I). Just because it’s rare for an innocent person’s DNA to match the crime scene, it doesn’t mean the person with a matching DNA is very likely guilty. This confusion is known as the prosecutor’s fallacy.
Let’s evaluate the above statement by calculating the P(I | ME).
The probability of the person is innocent $$P(I) = \frac{499999}{500000} = 0.999998$$
The probability of the person is not innocent $P(I^{c}) = \frac{1}{500000} = 0.000002$
The probability of the person is not innocent and having matching evidence $P(ME | I^{c}) = 1$
The probability of the person is innocent and having matching evidence $P(ME | I) = \frac{1}{100000} = 0.00001$
The probability of the having matching evidence
$$P(ME) = P(ME| I) P(I) + P(ME | I^{c}) P(I^{c})$$
$$P(ME) = 0.000012$$
The probability of the person is innocent given that he is having Matching Evidence $$P(I|ME) = \frac{P(ME/ I)*P(I)}{P(ME)} (Bayes’ Rule)$$
$P({I}| {ME})= 0.833333 >>>>>> P(ME / I) = 0.00001$
$P(I \mid ME)$ is 83%, which means that out of every 5 lakh people with a DNA match, approximately 5 are innocent and 1 is guilty.
References
https://repository.law.umich.edu/cgi/viewcontent.cgi?article=1059&context=mlr_fi