Imagine a bike racing competition.
Three riders are competing — each with a unique riding style:
- One is an Aggressive rider,
- Another is Aggressive and Far-sighted,
- And the third is Aggressive, Far-sighted, and Experienced.
All three start from the same distance away from the finish line.
Let’s understand how each rider reach the target— by comparing their riding style to P, PD, and PID controllers.
P Controller (Aggressive Rider)
Imagine a rider who only cares about how far he is from the target. The farther he is, the harder he accelerates — without worrying about his speed, balance, or whether he might overshoot. His only focus is closing the gap as fast as possible. He acts based purely on difference between the target and bike.
$$Throttling = (Aggressive-rider-factor)(Target_{position} – Current_{Bike position})$$
In Technical Language
$$u = Kp(z_{desired} – z_{actual})$$
The aggressiveness factor Kp, determines how hard he responds. Too aggressive? He ends up oscillating around the target.
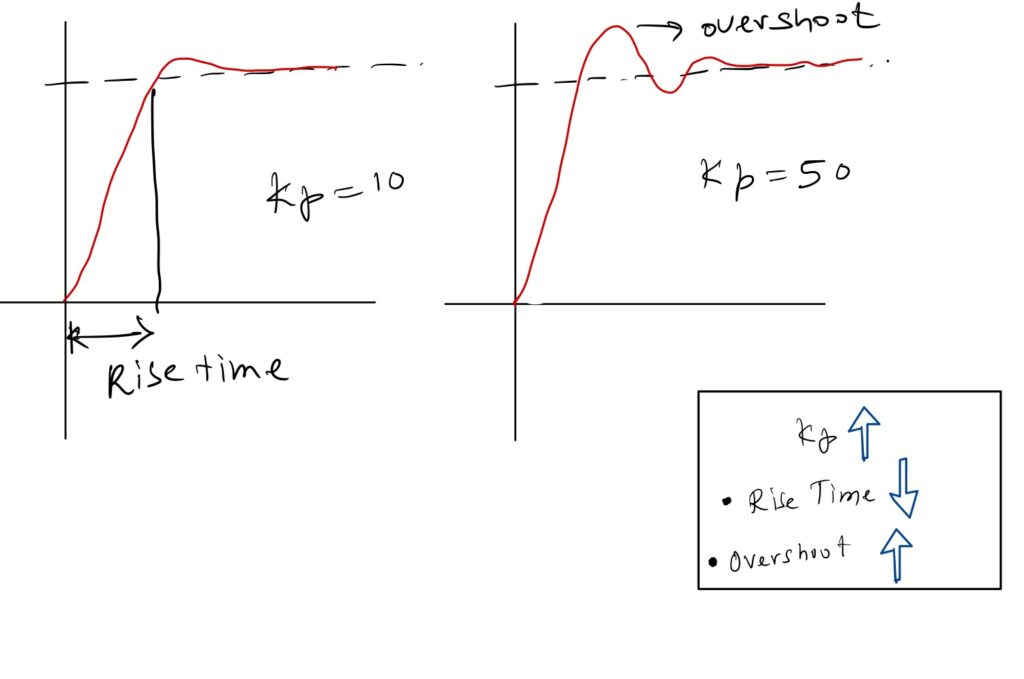
PD Controller (Aggressive + Far-Sighted Rider)
Now, think of a smarter rider. He not only looks at the distance to the target but also pays attention to his speed. If he’s going too fast as he approaches the target, he slows down early to stop exactly at the target without overshooting. He considers both current error and future (speed).
$$Throttling = (Aggressive-rider-factor)(Target_{Position} – Current_{Bike position}) + (Far-sighted-rider-factor)(Target_{Velocity} – Current_{Bike velocity})$$
In Technical Language
$$u = Kp(z_{desired} – z_{actual}) + Kd(\dot{z}_{desired} – \dot{z}_{actual})$$
A PD controller with high far-sight weightage (Kd) thinks too much about the future — so much so that he starts slowing down early and never fully reaches the target, leading to a steady-state error.
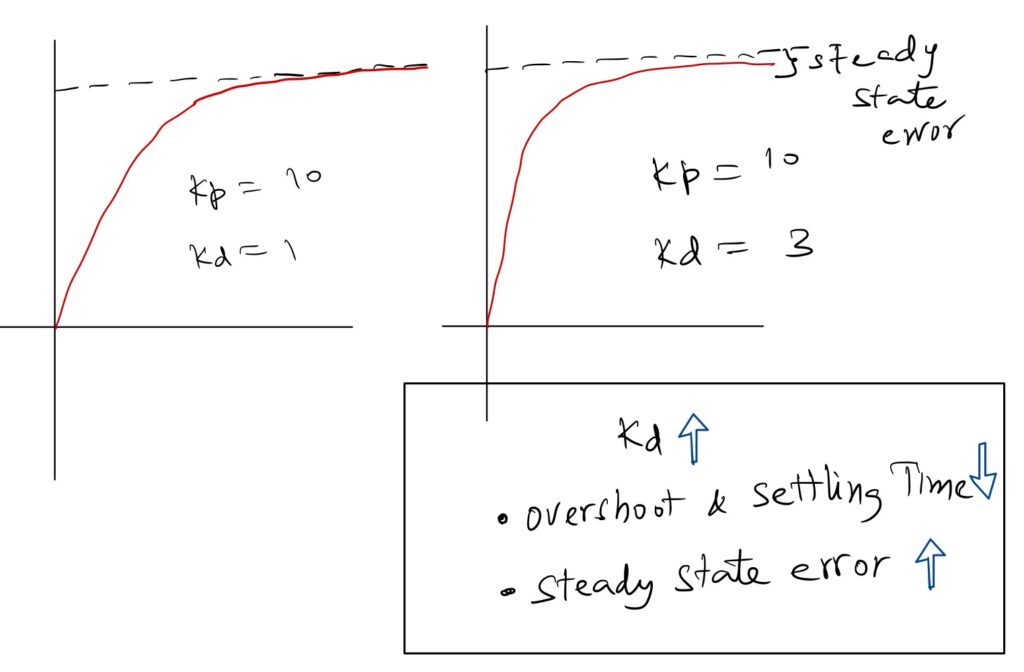
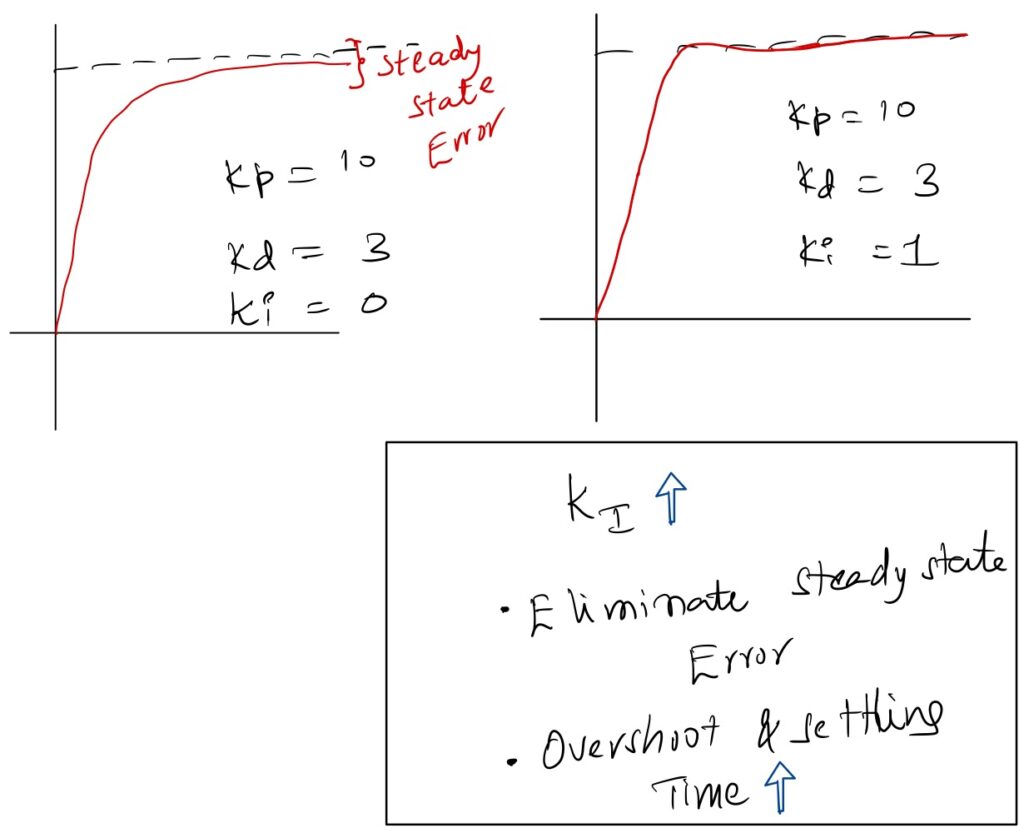
PID Controller (Aggressive+ Far-Sighted + Experienced Rider)
Finally, imagine a highly skilled rider. He remembers how he behaved in the past, watches his current distance and speed, and predicts what will happen next. He combines his past experience (integral), current situation (proportional), and future prediction (derivative) to reach the target smoothly and accurately
$$Throttling = (Aggressive-rider-factor)(Target_{Position} – Current_{Bike position}) + (Far-sighted-rider-factor)(Target_{Velocity} – Current_{Bike velocity})+$$
$$(Experienced-rider-factor)(\sum Position Error(Past Experience)$$
In Technical Language
$$u = Kp(z_{desired} – z_{actual}) + Kd(\dot{z}_{desired} – \dot{z}_{actual}) + Ki\int(z_{desired} – z_{actual}) $$
This (Aggressive, Far-Sighted, and Experienced) rider may take a little more time to reach the target, but he stops precisely where he should. He may overshoot slightly, but never falls short.
- Just like no single riding style fits every road, no single controller setting fits every system.
- Tuning the right mix of Kp, Kd and Ki based on your system’s behavior (plant dynamics) is essential. Overturning of any gain can lead to poor or unstable performance.