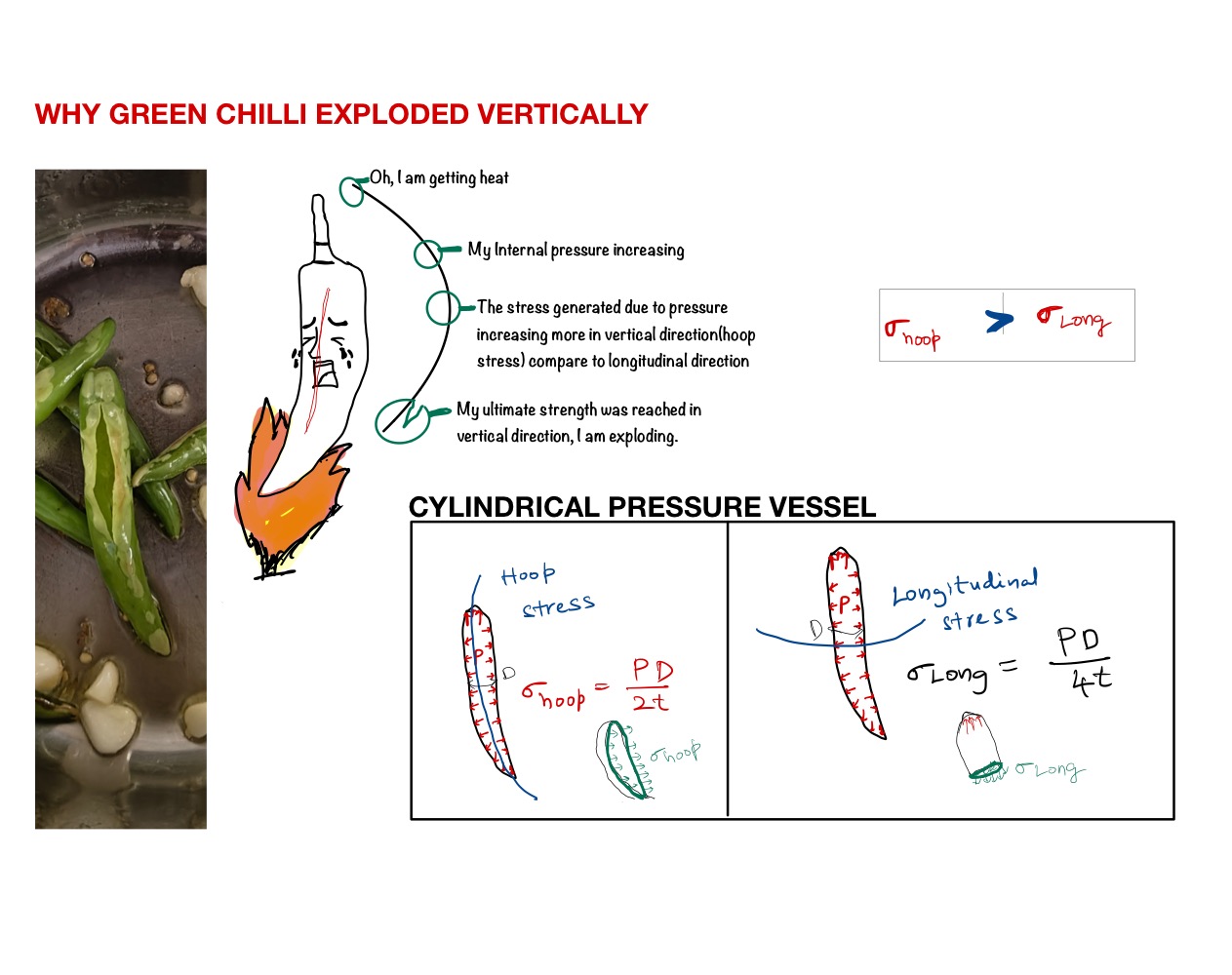
Learn about Longitudinal Stress and Hoop Stress of cylindrical pressure vessels by making tomato chutney.
A while back, I was making tomato chutney for the first time. As part of the preparation, I added some oil to a pan, removed the stalks from green chillies, and threw them directly into the hot oil. After a minute or two, they started exploding and splitting vertically, which I didn’t expect at all.
The moment I saw the green chillies explode, I remembered the reason behind it from a lecture on cylindrical pressure vessels during my bachelor’s. In that lecture, they had given the example of a hot dog splitting vertically. And in this post let’s understand the reason behind the vertical split of green chilli by assuming it as cylindrical pressure vessel.
Deriving Longitudinal and Hoop Stresses in Pressure Vessels
What is Stress
Stress is resistive force produced by the material over the area of cross section. If this stress exceed the strength of the material the material will go to permanent deformation.
It’s similar to the stress we experience daily due to external pressures. The amount of stress we take had certain limit, once it exceeds our capacity(strength), we also explode.
Longitudinal Stress
The stress acting along the longitudinal direction of the pressure vessel due to a applied pressure is called as longitudinal stress.
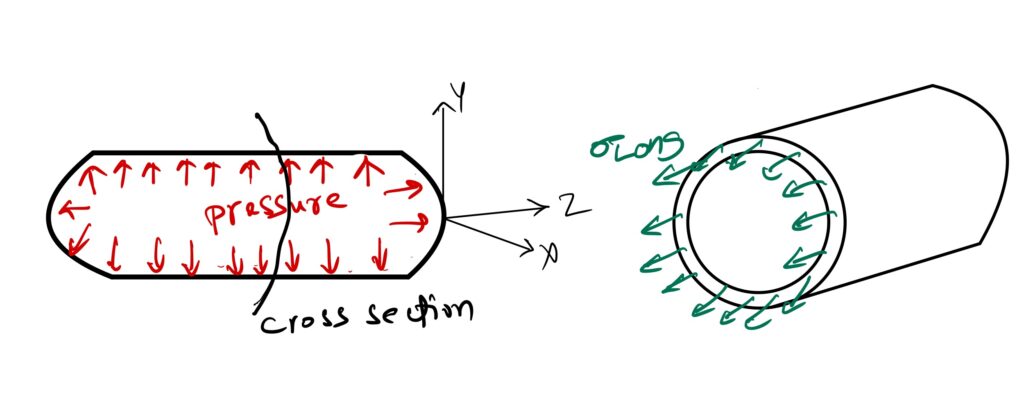
Summing the forces acting on the pressure vessel along the z-direction
$$\Sigma F_{z} = 0 $$
$$ \sigma_{Long}(2\pi rt) – P(\frac{\pi D^{2}}{4}) = 0$$
$$ \sigma_{Long}(2\pi rt) = P(\frac{\pi D^{2}}{4})$$
$$ \sigma_{Long}(2\pi (\frac{D}{2})t) = P(\frac{\pi D^{2}}{4})$$
$$ \sigma_{Long} = \frac{PD}{4t}$$
where,
D is the diameter of the pressure vessel,
t is thickness of the pressure vessel,
P is the pressure acting on the pressure vessel.
Hoop Stress
The stress acting along the circumference of the pressure vessel due to a applied pressure is called as hoop stress.
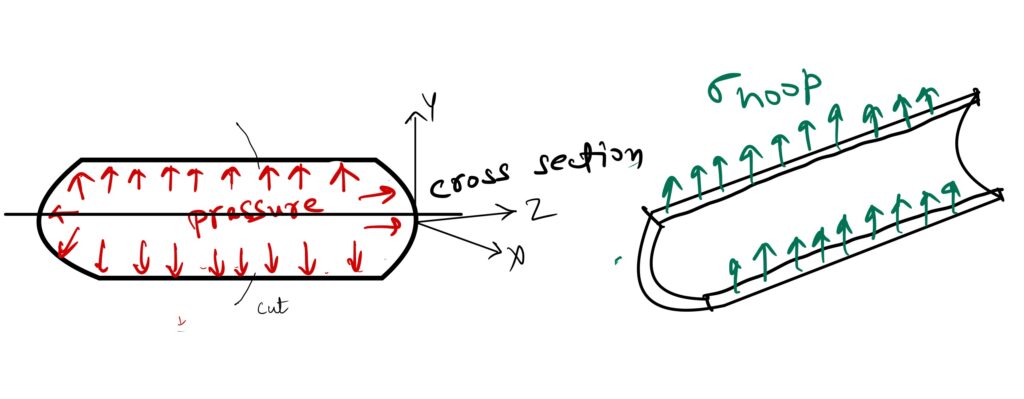
Summing the forces acting on the pressure vessel along the z-direction
$$\Sigma F_{y} = 0$$
$$ \sigma_{hoop}(2tL) – P(L)(D) = 0$$
$$ \sigma_{hoop}(2tL) = P(L)(D)$$
$$ \sigma_{hoop} = \frac{PD}{2t}$$
where,
L is the length of the pressure vessel.
From the above equations as pressure increases, The hoop stress increases more compare to longitudinal stress and fail along the circumference. This is why the green chilli in the figure above split vertically.